Matemática Avanzadas
viernes, 20 de diciembre de 2019
Funciones Inversas
Política de cookies: Las cookies de este sitio web se usan para personalizar el contenido y los anuncios, ofrecer funciones de redes sociales y analizar el tráfico. Además, compartimos información sobre el uso que haga del sitio web con nuestros partners de redes sociales, publicidad y análisis web, quienes pueden combinarla con otra información que les haya proporcionado o que hayan recopilado a partir del uso que haya hecho de sus servicios. Más información
Función inversa
Contenido de esta página:
- Definición de función
- Definición informal de inversa
- Definiciones previas
- Definición de función inversa
- Cuestiones sobre la inversa
- Obtención de la inversa
- Problemas resueltos
0. Definición de función
Una función de variable real, f:A→B, es una relación entre dos conjuntos A y B de los números reales que a cada número x de A le hace corresponder un único número de B, denotado por f(x) y llamado imagen de x mediante f.
De ahora en adelante, supondremos f:A→B, siendo A y B subconjuntos de los números reales R. A es el dominio de f y B es su codominio.Nota: B es el codominio y cumple f(A)⊆B. El conjunto f(A) es la imagen de f.
1. Definición informal de inversa
Informalmente, la función inversa de f es la función f−1:B→A tal que dado un número y de B, permite conocer el número x de A tal que y=f(x). Se escribe f−1(y)=x.
Ejemplo:
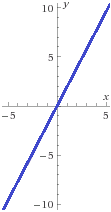
Si f(x)=2x, su inversa es f−1(x)=x/2. Por ejemplo,
f−1(8)=8/2=4
En efecto, la imagen de 4 es 8:
f(4)=2⋅4=8
Ejemplo:
Si f(x)=2x, su inversa es f−1(x)=x/2. Por ejemplo,
f−1(8)=8/2=4
En efecto, la imagen de 4 es 8:
f(4)=2⋅4=8

2. Definiciones previas
Ejemplo introductorio:
La función f(x)=x2 no tiene inversa ya que, por ejemplo, f−1(4) podría ser f−1(4)=2 o bien f−1(4)=−2:
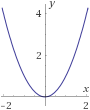 Nota: si restringimos el dominio de f a los reales no negativos o a los no positivos, la función sí tiene inversa.
Nota: si restringimos el dominio de f a los reales no negativos o a los no positivos, la función sí tiene inversa.
Teniendo en cuenta la definición dada para una función f, como f−1 también es una función, debe exigirse que cada número y de B tenga una única imagen x=f−1(y) en A. Al número x tal que f−1(y)=x se le denomina anti-imagen de y mediante f.
Matemáticamente, esta exigencia de la unicidad de la anti-imagen (para que sea una función) se traduce exigiendo que la función f sea inyectiva:
Matemáticamente, este problema se soluciona exigiendo que la función f sea sobreyectiva (o suprayectiva):
La función f(x)=x2 no tiene inversa ya que, por ejemplo, f−1(4) podría ser f−1(4)=2 o bien f−1(4)=−2:

Teniendo en cuenta la definición dada para una función f, como f−1 también es una función, debe exigirse que cada número y de B tenga una única imagen x=f−1(y) en A. Al número x tal que f−1(y)=x se le denomina anti-imagen de y mediante f.
Matemáticamente, esta exigencia de la unicidad de la anti-imagen (para que sea una función) se traduce exigiendo que la función f sea inyectiva:
La función f:A→B es inyectiva si cumple
f(x)=f(y)↔x=y,∀x,y∈A
Es decir, f es inyectiva si: la imagen de dos números de A son iguales si, y solamente si, dichos números de A son el mismo número.
Asimismo, como función, la inversa f−1 debe proporcionar la anti-imagen de todos los números de B. Sin embargo, esto no es posible si algún número de B no es la imagen de algún número de A.f(x)=f(y)↔x=y,∀x,y∈A
Es decir, f es inyectiva si: la imagen de dos números de A son iguales si, y solamente si, dichos números de A son el mismo número.
Matemáticamente, este problema se soluciona exigiendo que la función f sea sobreyectiva (o suprayectiva):
La función f:A→B es sobreyectiva (o suprayectiva) si cumple
∀y∈B, ∃x∈A, f(x)=y
Es decir, f es sobreyectiva si todo número de B es la imagen mediante f de algún número de A.
Debido a la importancia de la inyectividad y sobreyectividad de una función simultáneamente, existe una definición que considera ambas propiedades:∀y∈B, ∃x∈A, f(x)=y
Es decir, f es sobreyectiva si todo número de B es la imagen mediante f de algún número de A.
La función f:A→B es biyectiva si es inyectiva y sobreyectiva.
3. Definición de inversa
Veamos la definición formal de función inversa:
La función inversa f−1 de una función biyectiva f:A→B es la la función f−1:B→A que cumple
f−1(f(x))=x, ∀x∈A
f(f−1(y))=y, ∀y∈B
Dicho en otras palabras,
f−1∘f=idA
f∘f−1=idB
donde idA es la función identidad de A:
idA:A→A
idA(x)=x, ∀x∈A
e idB es la función identidad de B:
idB:B→B
idB(y)=y, ∀y∈B
f−1(f(x))=x, ∀x∈A
f(f−1(y))=y, ∀y∈B
Dicho en otras palabras,
f−1∘f=idA
f∘f−1=idB
donde idA es la función identidad de A:
idA:A→A
idA(x)=x, ∀x∈A
e idB es la función identidad de B:
idB:B→B
idB(y)=y, ∀y∈B
4. Cuestiones sobre la inversa
Cuestión 1
Si f−1:B→A cumple las condiciones dadas en la definición de función inversa de f, ¿es realmente la inversa de f? Es decir, ¿f−1 proporciona las anti-imágenes de f?∃y=f(x)∈B
En efecto, f−1 proporciona la anti-imagen de y aplicando la primera condición:
f−1(y)=f−1(f(x))=x
Cuestión 2:
¿La función inversa es única?Supongamos que la función g:B→A cumple las condiciones de la inversa de f.
Sea y un número de B. Como f es biyectiva, existe un número x de A tal que y=f(x).
Se tiene que
g(y)=x
Pero también,
f−1(y)=x
Por tanto,
g(y)=f−1(y), ∀y∈B
Esto demuestra que la inversa es única puesto que la imagen de cualquier número y de B mediante g coincide con la imagen mediante f−1. Es decir, las funciones son iguales porque están definidas entre los mismos conjuntos y la imagen de cada número de B coincide.
5. Obtención de la inversa
La definición de la inversa no indica cómo calcular la inversa de una función dada. El método que suele utilizarse es:
Si la expresión def:A→B es función de x, y=f(x), es suficiente con aislar x. Después, se cambia la x por la y y viceversa para obtener y=f−1(x).
Ejemplo:
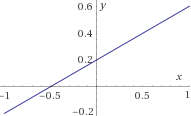
Sea la función biyectiva
f(x)=2x+15
 Para calcular f−1, aislamos x:
Para calcular f−1, aislamos x:
y=2x+15→
5y=2x+1→
5y−1=2x→
x=5y−12
Cambiamos x por y:
y=5x−12→
f−1(x)=5x−12
Si la expresión def:A→B es función de x, y=f(x), es suficiente con aislar x. Después, se cambia la x por la y y viceversa para obtener y=f−1(x).
Ejemplo:
Sea la función biyectiva
f(x)=2x+15

y=2x+15→
5y=2x+1→
5y−1=2x→
x=5y−12
Cambiamos x por y:
y=5x−12→
f−1(x)=5x−12
Para comprobar que f−1 es la inversa de f, hay que comprobar que se cumple
f−1(f(x))=x,∀x∈A
f(f−1(y))=y, ∀y∈B
f−1(f(x))=x,∀x∈A
f(f−1(y))=y, ∀y∈B
6. Problemas Resueltos
Problema 1
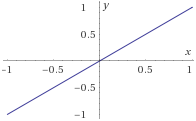
Determinar cuáles de las siguientes funciones tienen o no tienen inversa y por qué. No es necesario calcular la inversa:- f1:R→R definida por
f1(x)=x
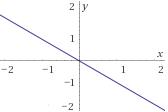
- f2:R→R definida por
f2(x)=−x
- f3:R→R definida por
f3(x)=x2

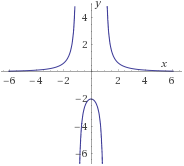
- f4:R−{±1}→R definida por
f4(x)=2x2−1
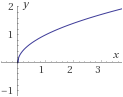
- f5:[0,+∞)→R definida por
f5(x)=√x
- f6: :R−{−1}→R definida por
f6(x)=x2x+1
Ayuda: considerar f−1(−1).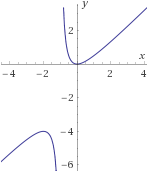
Solución
Problema 2
La biyectividad y, por tanto, la existencia de función inversa, depende de los conjuntos A y B entre los que se define una función.Las siguientes funciones f:A→B son sobreyectivas, pero no tienen inversa porque no son inyectivas. Encontrar, para cada función, el mayor dominio C⊂A para que las funciones f|C sí tengan inversa.
f|C:C→B
f|C(x)=f(x), ∀x∈C
Nota: la función f|C es la función f restringida al subconjunto C del dominio A de f.
Funciones:
- f1:R→[0,+∞) definida por
f1(x)=x2

- f2:R→[0,+∞) definida por
f2(x)=|x|
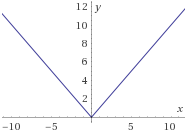
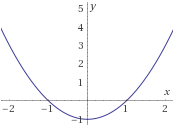
- f3:R→[−1,+∞) definida por
f3(x)=x2−1
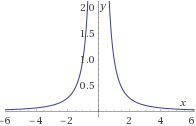
- f4:R−{0}→(0,+∞) definida por
f4(x)=1x2
- f5,f6:[−2π,2π]→[−1,1] definidas por
f5(x)=cos(x)
f6(x)=sin(x)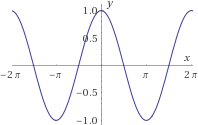
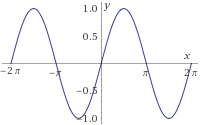
Solución
Problema 3
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f1(x)=x3
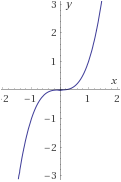
Solución
Problema 4
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f2(x)=x4
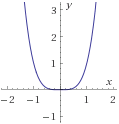
Solución
Problema 5
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f3(x)=1+x2+2x3+3x5
Solución
Problema 6
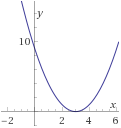
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f4(x)=x2−6x+9
Solución
Problema 7
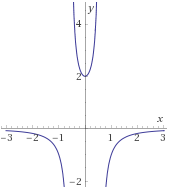
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f5(x)=21−3x2
Solución
Problema 8
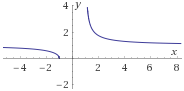
Encontrar la inversa de la siguiente función y demostrar (o comprobar) que lo es:f6(x)=√x+1x−1
Solución
Problema 9
Relacionar las siguientes funciones- f1(x)=sin(x)
- f2(x)=ex
- f3(x)=3√x
- f4(x)=1x
- f5(x)=tan(x)
- f6(x)=x
- f7(x)=1√x
- fa(x)=x3
- fb(x)=arctan(x)
- fc(x)=ln(x)
- fd(x)=1x2
- fe(x)=arcsin(x)
- ff(x)=1/x
- fg(x)=x
Solución

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Suscribirse a:
Entradas (Atom)




